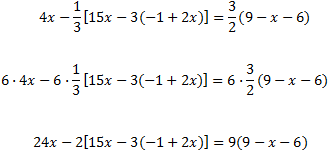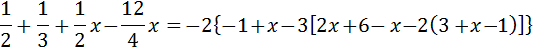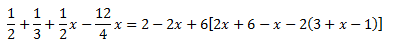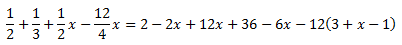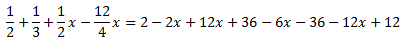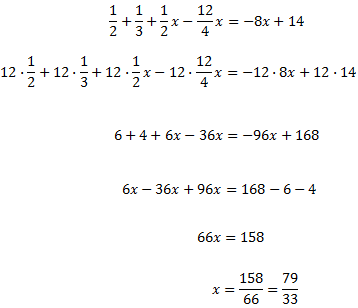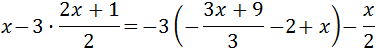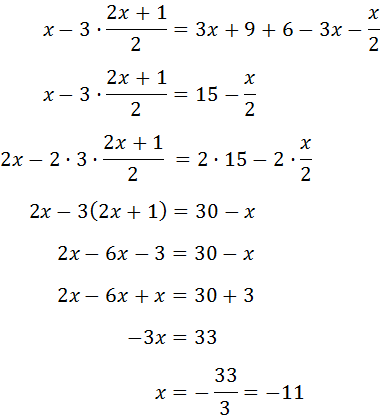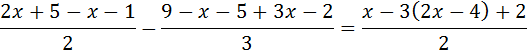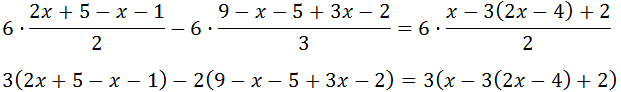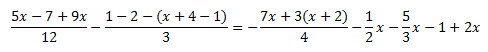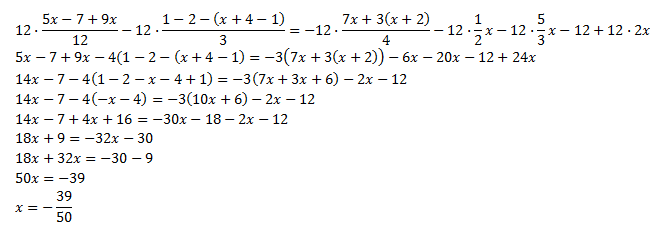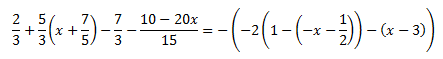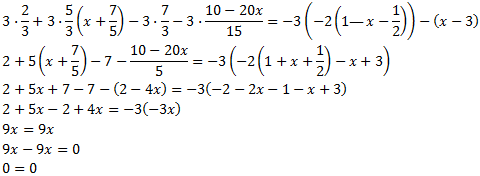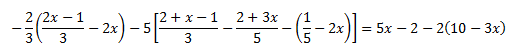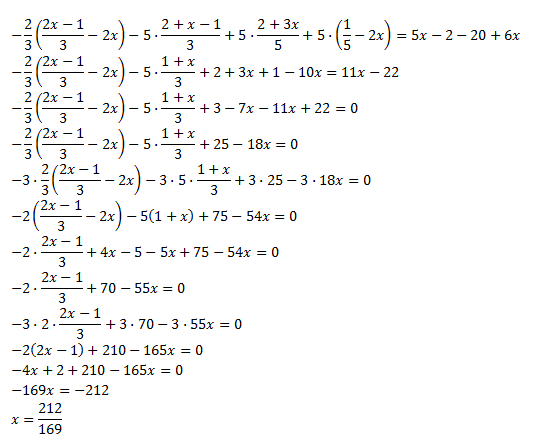Contenido de esta página:
- Breve Introducción
- Recordemos que... (tipos de soluciones, paréntesis y fracciones)
- Ecuaciones de Primer Grado Resueltas paso a paso
Introducción
En cuanto a las matemáticas, las ecuaciones de primer grado son la
introducción al álgebra. Su comprensión es imprescindible para cualquier
tipo de ecuaciones: ecuaciones de segundo grado o de grado mayor,
exponenciales,
irracionales, etc. y para los sistemas de ecuaciones.
En cuanto a la vida real, aunque en un principio no se piense así,
las ecuaciones
son una herramienta de gran utilidad que nos permiten resolver
numerosos problemas a los que nos enfrentamos diariamente.
Como ya indica su nombre, en las ecuaciones de primer grado, la parte literal de los monomios no tiene exponente (por ejemplo, 3x puede formar parte de una ecuación pero 3x2
no porque sería de segundo grado). Justamente este hecho nos asegura
que, en caso de existir solución, hay sólo una (excepto el caso especial
en qué hay infinitas soluciones).
Decimos "en caso de existir solución" ya que en ocasiones las ecuaciones no tienen solución. Por ejemplo, la ecuación x = x + 1
(cuya lectura es "un número que es igual a su consecutivo") no tiene
solución porque esto nunca se cumple. De hecho, la ecuación se reduce a 1
= 0, lo cual es imposible.
Recordemos que...
- Si obtenemos una igualdad imposible,
la ecuación no tiene solución.
Ejemplo:
Si obtenemos la ecuación 1 = 0 , la ecuación inicial no tiene solución.
- Si obtenemos una igualdad que siempre se cumple,
cualquier valor es solución de la ecuación, es decir, la solución es todos los reales.
Ejemplo:
Si obtenemos la igualdad 0 = 0 , la solución es todos los reales:
x∈R
- Cuando hay denominadores y queremos evitarlos,
multiplicamos toda la ecuación por el mínimo común múltiplo de éstos.
De este modo, al simplificar, los denominadores desaparecen.
Para quitar los paréntesis,
multiplicamos el coeficiente de delante del paréntesis por todos los elementos que contiene.
El coeficiente puede ser el signo menos (es decir, -1, entonces el contenido cambia de signo),
el signo más (es decir, +1, el contenido no cambia) o un número positivo, negativo o una fracción
(este número pasa a multiplicar todo el contenido del paréntesis,
cambiando los signos en el caso de ser negativo).
Cuando tenemos paréntesis anidados, es decir, un paréntesis dentro
de otro, los vamos quitando desde fuera hacia dentro. Es decir, primero
quitamos el paréntesis exterior (multiplicando su contenido por su coeficiente) y
después, quitamos los siguientes procediendo del mismo modo: desde el más exterior
a los más interiores. En realidad,
no es necesario seguir un orden a la hora de quitar los paréntesis, pero es
recomendable seguirlo mientras estamos aprendiendo.
En esta sección se resuelven ecuaciones de primer grado cuya
dificultad va aumentado: ecuaciones simples, con fracciones (donde
usaremos el mínimo común múltiplo), con paréntesis y con paréntesis
anidados
(unos dentro de otros).
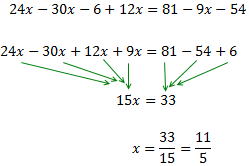
Ecuación 1
Sumamos (o restamos) los monomios con la misma parte literal (las x con x, los números con números). Los que están sumando en un lado, pasan al otro lado restando y viceversa.
Después pasamos las x a un lado de la igualdad y los números a la otra.
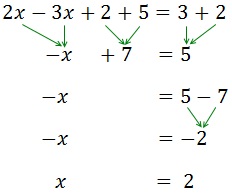
Ecuación 2
Los elementos que están sumando en un lado, pasan al otro lado restando y viceversa.
Después pasamos las x a un lado de la igualdad y los números a la otra.
Ecuación 3
Primero nos deshacemos del paréntesis: como tiene un signo
negativo delante, cambiamos el signo a todos los elementos de su
interior.
Luego sólo tenemos que agrupar las x en un lado y los números en el otro.
Como la x tiene un coeficiente (2) multiplicando, éste pasa al otro lado dividiendo.
Ecuación 4
Solución
Primero nos deshacemos de los paréntesis: el de la derecha
tiene un signo negativo, que cambia el signo de los elementos del
interior; el de la derecha está multiplicado por 3, que pasa dentro del
paréntesis multiplicando a todos los elementos.
Ecuación 5
Solución
Tenemos fracciones. Podemos proceder de varias formas:
- multiplicar todos los términos de la ecuación por el mínimo común múltiplo de los denominadores
- o bien, ir multiplicando por cada denominador.
Nosotros multiplicamos toda la ecuación por el mínimo común múltiplo, que es 6:
De este modo, al efectuar la división, desaparecen los denominadores.
Ahora nos deshacemos de los paréntesis: el primero está
multiplicado por 3, por lo que multiplicamos por 3 su contenido; el
segundo por -2, por lo que multiplicamos por -2 (no olvidar el signo):
Finalmente, agrupamos las x a un lado y los números al otro:
Tenemos 0 = -2, lo cual es una igualdad falsa. Por tanto, la ecuación no tiene solución porque sea cual sea el valor de x, llegamos a una relación (igualdad) absurda.
Ecuación 6
Solución
Los números que multiplican a los paréntesis son negativos,
con lo que al multiplicar su contenido por éstos, todos los elementos
cambian de signo.
Ecuación 7
Solución
Como tenemos denominadores, multiplicamos toda la ecuación por el mínimo común múltiplo de éstos, que es 6:
De este modo, al efectuar las divisiones, desaparecen los denominadores.
Ahora sólo falta agrupar las x a un lado y los números al otro.
Ecuación 8
Solución
Como tenemos denominadores, multiplicamos toda la ecuación por el mínimo común múltiplo de estos, que es 30:
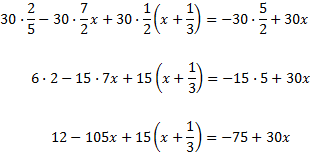
Sólo tenemos un paréntesis, que está multiplicado por 15. Para quitarlo, multiplicamos su contenido por 15:
Ecuación 9
Solución
En la ecuación tenemos paréntesis anidados (unos dentro de
otros) y multiplicados por fracciones. Pero antes de ocuparnos de esto,
multiplicamos toda la ecuación por el mínimo común múltiplo de los
denominadores, que es 6:
Ahora vamos a los paréntesis:
En la izquierda hay dos, pero lo tratamos como si fuera sólo uno. Es decir, multiplicamos todo su contenido por -2.
Al mismo tiempo, en la derecha, multiplicamos el contenido por 9:
Nos queda un paréntesis, que está multiplicado por 6:
Ecuación 10
Solución
Como tenemos paréntesis anidados (uno dentro de otro), vamos a ir quitándolos.
El primer paréntesis (el exterior), está multiplicado por -2. Para quitarlo, multiplicamos todo su contenido por -2:
Ahora, el paréntesis exterior está multiplicado por 6. Para quitarlo, multiplicamos su contenido por 6:
Por último, el paréntesis que queda está multiplicado por -12, por lo que para quitarlo multiplicamos por -12 su contenido:
Ahora vamos a deshacernos de las fracciones, pero antes, sumamos algunos elementos para no tener una expresión tan larga:
Multiplicamos toda la ecuación por el mínimo común múltiplo de los denominadores, que es 12:
Ecuación 11
Solución
Hemos decidido deshacernos primero del paréntesis y, después, evitar las fracciones multiplicando por los denominadores: 2.
Ecuación 12
Solución
La ecuación consta sólo de 3 fracciones, así que la multiplicamos por el mínimo común múltiplo de los denominadores.
Ecuación 13
Solución
Multiplicamos por el mínimo común múltiplo de los denominadores.
Ecuación 14
Ver Solución
En este ejercicio hemos multiplicado por un denominador,3,
y después al desarrollar los paréntesis anidados y simplificar,
desaparecen las fracciones.
Hemos llegado a una igualdad que siempre es verdadera y no depende de
x. Esto significa que sea cual sea el valor de x,
siempre se cumple la ecuación.
Por tanto, la solución es todos los números reales (infinitas
soluciones):
x∈R
Ecuación 15
Solución
Tenemos paréntesis anidados y fracciones.
Hemos simplificado los paréntesis y, después, hemos multiplicado la
ecuación por alguno de los denominadores según nos interesaba para
evitar las fracciones.
MATERIAL PROPORCIONADO POR:













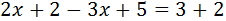
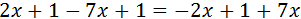
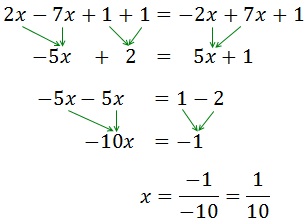
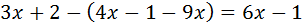
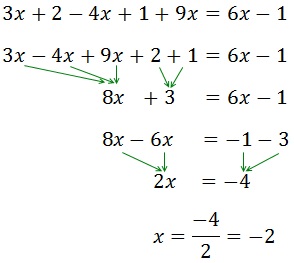
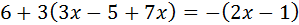
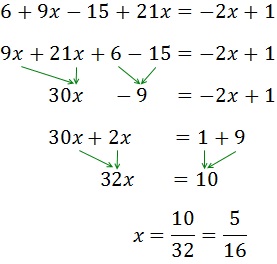
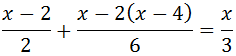
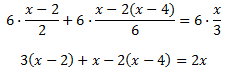
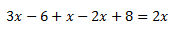
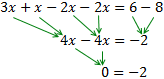
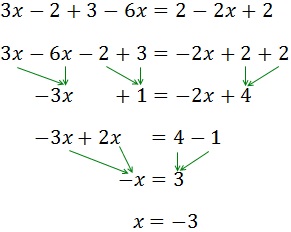
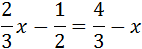
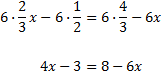
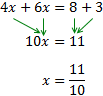
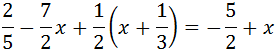
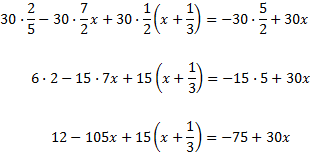
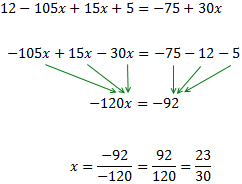
![ecuación de primer grado con paréntesis anidados (uno dentro de otro): 4x - (1/3)[15x-3(-1+2x)] = (3/2)(9-x-6) ecuaciones de primer grado resueltas](https://www.matesfacil.com/ESO/Ecuaciones/Ecua9.jpg)